给亲戚家孩子补习初中课程，好多东西都忘记了。故翻看教材，整理和回顾一下知识点。

数学（冀教版）

七年级上

第1章 有理数

第2章 几何图形的初步认识

第3章 代数式

第4章 整式的加减

第5章 一元一次方程

七年级下

第6章 二元一次方程组

第7章 相交线与平行线

第8章 整式的乘法

第9章 三角形

第10章 一元一次不等式和一元一次不等式组

第11章 因式分解

八年级上

第12章 分式和分式方程

第13章 全等三角形

第14章 实数

第15章 二次根式

第16章 轴对称和中心对称

第17章 特殊三角形

八年级下

第18章 数据的收集与整理

第19章 平面直角坐标系

第20章 函数

第21章 一次函数

第22章 四边形

九年级上

第23章 数据分析

第24章 一元二次方程

第25章 图形的相似

第26章 解直角三角形

第27章 反比例函数

第28章 圆

九年级下

第29章 直线与圆的位置关系

第30章 二次函数

第31章 随机事件的概率

第32章 投影与视图

数学（人教版）

七年级上

第1章 有理数

第2章 整式的加减

第3章 一元一次方程

第4章 几何图形初步

七年级下

第5章 相交线与平行线

第6章 实数

第7章 平面直角坐标系

第8章 二元一次方程组

第9章 不等式与不等式组

第10章 数据的收集、整理与描述

八年级上

第11章 三角形

第12章 全等三角形

  • 12.1 全等三角形
    • 全等形，全等三角形
    • 对应顶点，对应边，对应角
    • ABC与DEF全等，记作△ABC≌△DEF
    • 全等三角形的对应边相等，对应角相等
  • 12.2 三角形全等的判断
    • 三边分别相等的两个三角形全等（边边边）
    • 两边和它们的夹角分别相等的两个三角形全等（边角边）
    • 两角和它们的夹边分别相等的两个三角形全等（角边角）
    • 两角和其中一个角的对边分别相等的两个三角形全等（角角边）
    • 斜边和一条直角边分别相等的两个三角形全等（斜边直角边）
  • 12.3 角的平分线的性质

第13章 轴对称

第14章 整式的乘法与因式分解

第15章 分式

八年级下

第16章 二次根式

第17章 勾股定理

第18章 平行四边形

第19章 一次函数

第20章 数据的分析

九年级上

第21章 一元二次方程

第22章 二次函数

第23章 旋转

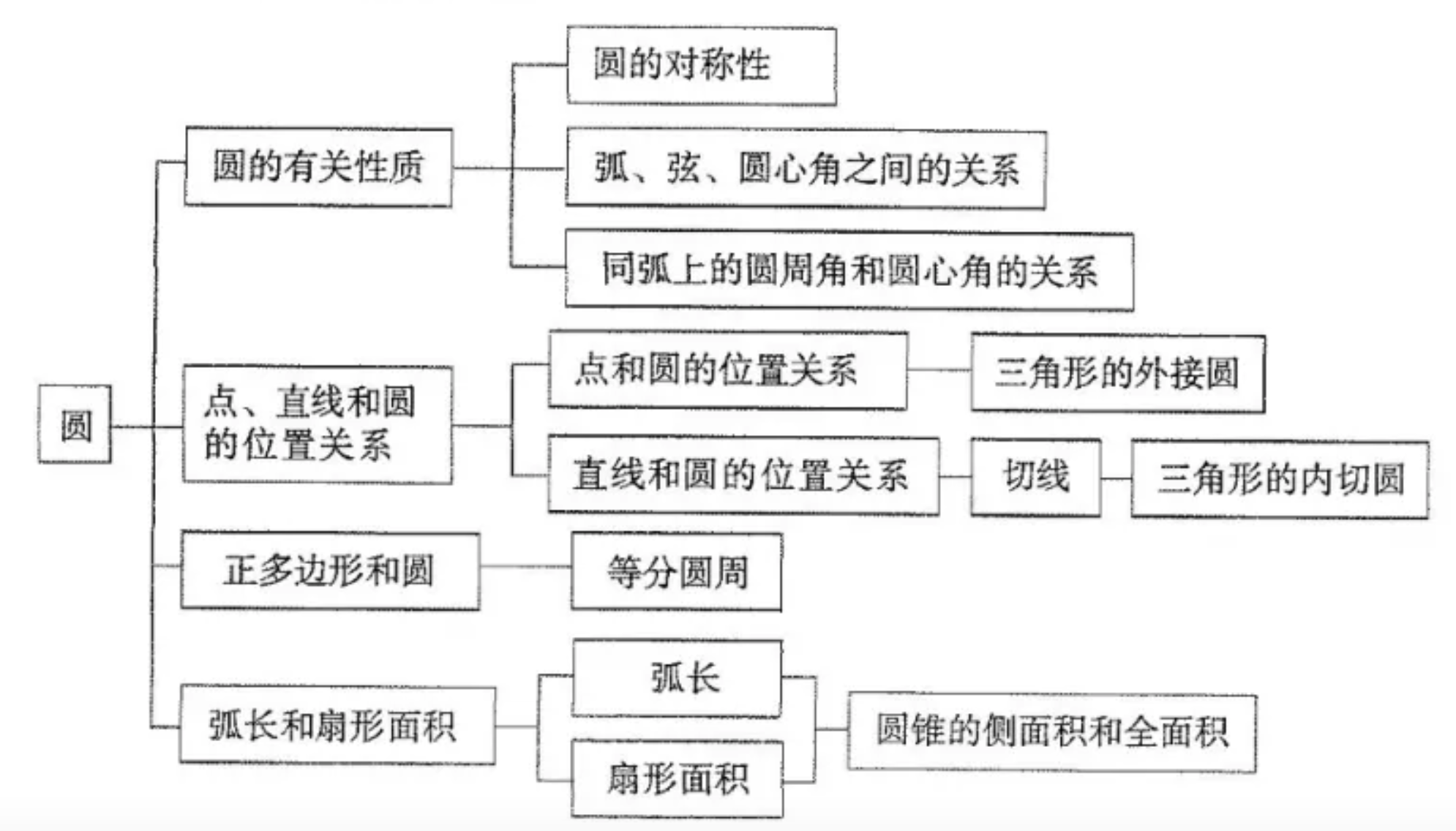
第24章 圆

  • 24.1 圆的有关性质
    • 24.1.1 圆
      • 圆，圆心，半径，记作⊙O，读作“圆O”
      • 弦，直径
      • 圆弧/弧，半圆，优弧和劣弧
      • 等圆（能够重合的两个圆），等弧
    • 24.1.2 垂直于弦的直径
      • 轴对称图形，直径为对称轴
      • 垂直于弦的直径 => 平分弦，平分弧
      • 平分弦的直径 => 垂直于弦，平分弧
    • 24.1.3 弧、弦、圆心角
      • 圆心角（定点在圆心上）
      • 在同圆或者是等圆中：
        • 角等 => 弦等，弧等
        • 弦等 => 角等，弧等
        • 弧等 => 角等，弦等
    • 24.1.4 圆周角
      • 圆周角：顶点在圆上，并且两边都与圆相交
      • 圆周角定律：
        • 同弧所对圆周角为其圆心角的一半
        • 同弧或等弧所对的圆周角相等
        • 半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径
      • 圆内接多边形，多边形的外接圆
      • 圆内接四边形的对角互补（和为180度）
  • 24.2 点和圆、直线和圆的位置关系
    • 24.2.1 点和圆的位置关系
      • 设圆O半径为r，点P到圆心的距离OP=d，则
        • 点P在圆外 <=> d>r
        • 点P在圆上 <=> d=r
        • 点P在圆内 <=> d<r
      • 不在同一条直线上的三个点确定一个圆，这个圆叫外接圆，其圆心为三角形的外心（三边垂直平分线的交点）
    • 24.2.2 直线和圆的位置关系
      • 相交（割线），相切（切线，切点），相离
      • 设圆O半径为r，圆心O到直线的距离为d：
        • 相交 <=> d<r
        • 相切 <=> d=r
        • 相离 <=> d>r
      • 切线的判定定理：经过半径的外端且垂直于这条半径的直线
      • 圆的切线垂直于过切点的半径
      • 圆外一点的两条切线，切线长
      • 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角
      • 内切圆，内心（三条角平分线的交点）
      • 圆与圆的关系：外离，内含，相切（内切和外切），相交
  • 24.3 正多边形和圆
    • 正多边形的中心，半径，中心角，边心距
  • 24.4 弧长和扇形面积
    • 360度的圆心角所对应的弧长：2πR
    • n度的圆心角对应的弧长：2πR/360*n
    • 扇形：n度圆心角的扇形面积：nπR^2/360
    • 圆锥，母线，全面积

第25章 概率初步

  • 25.1 随机事件与概率
    • 25.1.1 随机事件
    • 25.1.2 概率
  • 25.2 用列举法求概率
  • 25.3 用频率估计概率

九年级下

第26章 反比例函数

第27章 相似

第28章 锐角三角形

第29章 投影与视图